By Robert Pyke Ph.D., G.E.
The short answer to the question “what is the difference between 2D and 3D analyses of slope stability by the Method of Slices” is that it can be significant and varies in surprising ways. The examples below illustrate some of the differences, but these are just the tip of the iceberg. Results are given for analyses using the new computer program TSLOPE and using both the Ordinary Method of Columns (OMC) and Spencer’s Method so that these examples also illustrate the differences between results obtained by these two methods. In two companion articles and in Pyke (2017a) and Pyke (2017b) it is explained why previous criticisms of the Ordinary Method of Slices (OMS), of which the OMC is a 3D extension, are misplaced and it is shown that if the alternate method of specifying unit weights described by both Whitman and Bailey (1967) and Duncan, Wright and Brandon (2014) is used, very reliable results are obtained. It turns out that any differences between the OMS and the OMC and methods of analysis that “fully satisfy equilibrium” are due not to how unit weights and hydrostatic pore pressures are treated but to the different distributions of normal stresses around the potential slip surface. While solutions that “fully satisfy equilibrium” such as Spencer’s Method have been favoured by academics, the OMC turns out to have some practical advantages including its ability to compute and display local factors of safety, which may indicate the likelihood of progressive failure, the inclusion of seepage forces, and greater clarity in modelling applied loads and internal reinforcing.
- Hungr et al. Example No. 1
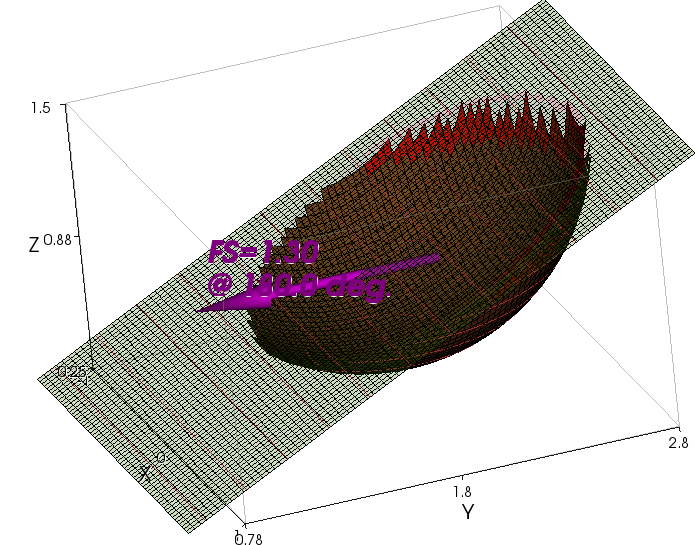
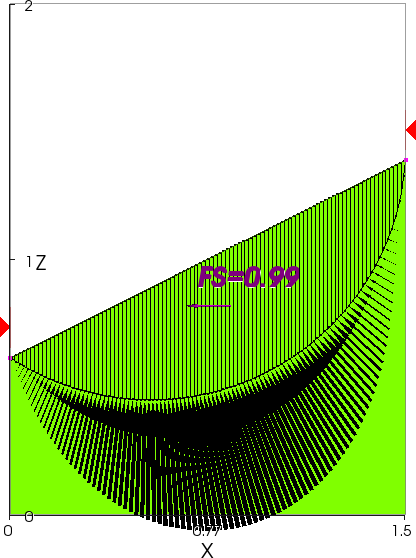
This example, from the paper by Hungr, Salgado and Byrne (1989), has a spherical slip surface that cuts into a planar slope. The original problem had a homogeneous frictionless soil with a value of cohesion that was reported to give a factor of safety of 1.402 according to a “closed-form” solution. The problem and the solution obtained using the OMC is shown in Figure 4(a).
Figure 4(a) – Hungr et al. Problem – OMC Solution
The factor of safety of 1.35 is slightly less than the theoretical factor of safety of 1.40 because constant width columns that fit entirely within the spherical slip surface were used, leaving small patches of the spherical surface to which the cohesion was not applied. A factor of safety of 1.30 was obtained using Spencer’s Method.
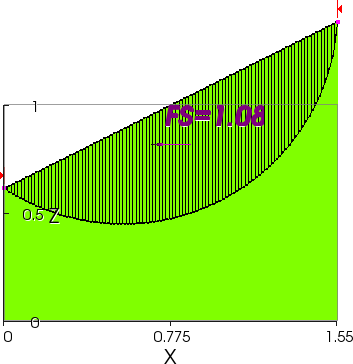
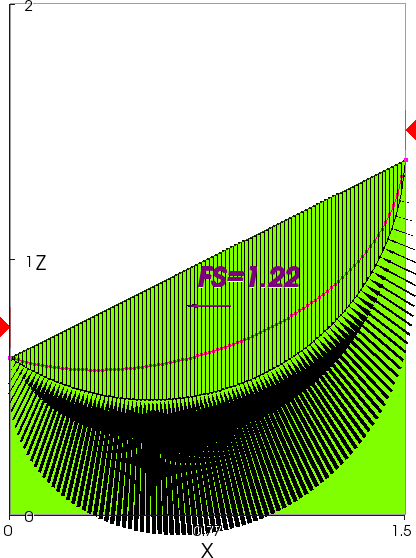
In 2D both the OMC and Spencer give the same answer, as shown below in Figures 4(b) and (c), even though the computed stresses around the slip surface are different and the Spencer solution shows significant tension. This occurs because the strength is specified only as a cohesion and the factor of safety is close to one. But note the difference between the 2D and 3D answers. The 3D solution gives a factor of safety that is some 25 percent higher than the 2D solution. This should not come as a surprise because it is entirely consistent with the well-known technical note by Baligh and Azzouz (1975) on end effects, but it probably does come as a surprise to many engineers who would assume that a 2D analysis through a slope with a constant cross section will provide the correct answer. It turns out that it does not in all cases. In particular, significant errors can arise when trying to compute soil properties by using back analyses of failures because a 2D solution may give back-calculated properties that are too high or too low. Back-calculated properties can be even more in error if the failure has an aspect ratio of less the one, as is more typically the case, rather than being spherical.
Figure 4(b) – 2D Solution by OMC
Figure 4(c) – 2D Solution by Spencer’s Method
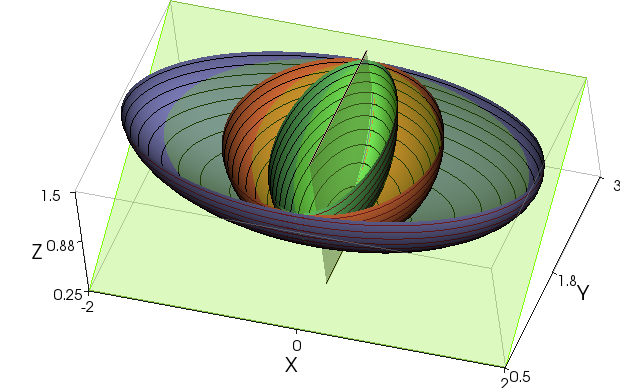
Figure 4(d) shows a top view of a family of three ellipsoids with the middle one being the same as the sphere in Figure 4(a) and the inner and outer ellipsoids having aspect ratios of 0.5 and 2.0 respectively.
Figure 4(d) – Family of Ellipsoids
Table 4 – Factors of Safety for Hungr et al. Example 1
The computed factors of safety for these three ellipsoids along with the 2D case are shown in Table 4. It may be seen that for an aspect ratio of 0.5, the 3D factor of safety is now 50 percent greater than the 2D solution. As the aspect ratio increases, the “end effects” diminish and the factor of safety for an ellipsoid approaches the 2D factor of safety. Many, or even most, natural landslides have aspect ratios of less than one being controlled by local weaknesses in structure, material properties or water conditions and accurate reconstruction or prediction of failures requires a 3D analysis.
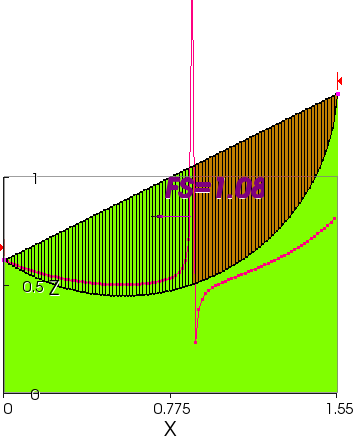
Going back to examine the 2D solutions in more detail, it can be seen that the interslice forces in the Spencer’s Method solution are in tension in the upper half of the potential sliding mass. While not shown in these figures, in the OMC solution the local factors of safety are correspondingly less than one in the upper half of the potential sliding mass. The line of thrust in the solution by Spencer’s method of course is not tenable, but that is of no great consequence in this limited instance. However, if the material is assumed to be cohesionless and to have shear strengths that vary with the normal effective stress on the slip surface, the load redistribution that takes place in Spencer’s Method in order to force the factor of safety to be the same on the base of each slice, leads to a reasonable line of thrust but also a calculated factor of safety that diverges from that obtained by the OMC, as shown in Figures 4(e) and (f).
Figure 4(e) – 2D Solution by OMC, c=0, φ=20 degrees
Figure 4(f) – 2D Solution by Spencer’s Method, c=0, φ=20 degrees
The black arrows in these figures indicate the effective normal stresses on the base of each slice. It is not possible to say which of the solutions shown in Figures 4(e) and (f) is the “more correct”. If the potential sliding mass is more like a rigid body the Spencer’s solution, which is kinematically admissible in this case, may be “more correct” and if the potential sliding mass is deformable, if for instance it is composed of sand particles, the OMC solution may well be “more correct”
The differences between both 2D and 3D analyses with an aspect ratio of one and the two solution methods are further illustrated in Tables 5(a) and 5(b). Table 5(a) shows the calculated factors of safety for three values of cohesion and Table 5(b) shows the calculated factors of safety for three values of the angle of friction.
Table 5(a) – Factors of Safety for All Cohesion
Table 5(b) – Factors of Safety for All Friction
Several interesting things can be seen in these two tables. In Table 5(a) it can be seen that when the shear strengths are specified as fixed numbers, the OMC and Spencer’s method give essentially the same answer. And, for this geometry, when the shear strengths are specified as fixed numbers, the 3D factor of safety is about 25 percent greater than the 2D factor of safety. In Table 5(b) it can be seen that when the shear strengths are a function of the effective stresses on the bases of the slices or columns, the OMC gives a factor of safety that is about 25 percent less than Spencer’s method in 2D analyses and 40 percent less in 3D analyses. 3D analyses give factors of safety by Spencer’s Method that are essentially the same as those from 2D analyses and the 3D factors of safety by the OMC are about 10 percent less than those computed in 2D analyses. The reason for this last result is simply that the slices in the 2D section down the centre of the spherical slip surface have higher effective stresses at the base than do the columns in the 3D analysis which shorten as they move out to the perimeter of the potential sliding mass.
So, at least an interim conclusion that can be drawn from this example is that simple rules on the effects of different methods of analysis and 3D effects are likely to be misleading and the engineer both has to keep his or her wits about themselves and test alternate solutions to their particular problem. If you don’t do that, you will never know what the possible errors might be.
This example was confined to simple circular, spherical or ellipsoidal slip surfaces. The next two examples illustrate the possible effects of natural and man-made 3D topography.
- Kettleman Hills Landfill Failure
An early example of the analysis of 3D effects on real world problems was provided by the failure of the liner system at the Kettleman Hills hazardous waste landfill, reported by Mitchell et al. (1990) and Seed et al. (1990) and summarized and updated by Duncan, Wright and Brandon (2014, pp. 32 and 282). As may be seen in Figure 5(a), the initial landfill was placed against liners on one side and one end of what was to be a completely lined basin. Because the liner had not been completed on the left hand side of the basin, which is at the top of the figure, the landfill had a partially free face on that side, as well as on the front.
Figure 5(a) – 3D View of Kettleman Hills Landfill
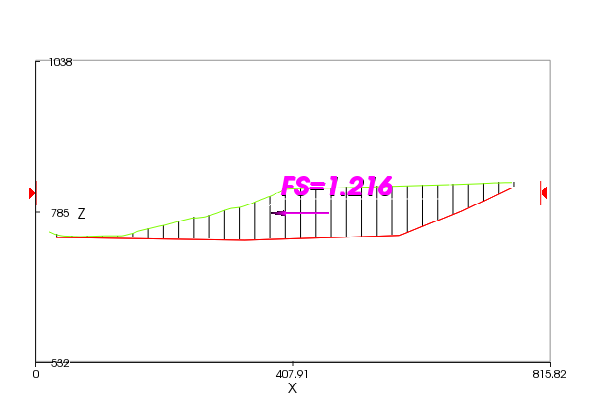
When the landfill had reached a maximum height of 90 feet, a slope failure occurred with horizontal and vertical movement of up to 14 and 35 feet. Subsequent investigations suggested that the basic failure occurred along a wetted HDPE liner compacted clay layer interface which resulted from the clay layer having been placed wet of optimum moisture content and then subsequent consolidation with drainage restricted by the HDPE liner. The extent of this wetted interface condition was not clear, thus Seed et al. (1990) conducted stability analyses for both partial and full wetting of the base. For a number of 2D cross sections, Seed et al. (1990) obtained factors of safety of 1.2 to 1.25 for the partial base wetting case and 1.10 to 1.15 for the full base wetting case. For the diagonal 2D cross-section that is shown in Figures 5(a) and (b), drawn in the direction of movement indicated by a 3D analysis, TSLOPE gives 2D factors of safety of 1.21 and 1.22 for the OMC and Spencer’s Method respectively, assuming full base wetting.
Figure 5(b) – Analysis of 2D Section by Spencer’s Method
Table 6 – Calculated Factors of Safety
Seed et al. then explored 3D effects by conducting what they described as a “force-equilibrium analysis” using five blocks and obtained 3D factors of safety of 1.08 and 1.01 for the partial and full base wetting cases. Assuming full base wetting, TSLOPE gives factor of safety of 1.00 and 1.05 by the OMC and Spencer’s method respectively, as listed in Table 6. Thus, making normal judgments about the appropriate 2D section to analyse, the 3D factor of safety appears to be 10-20 percent below the 2D factor of safety. The reason for the lower 3D factor of safety can be explained in either of several ways. One way is to say that because of the longer back slope relative to the base area, there is more “push” from the slope relative to the resistance provided by the base. Alternately, one can view this as a problem where the “end effects” are less than they would be in a long slope with a constant 2D cross section. The 10 to 20 percent difference may or may not be a big deal from the design point of view because the failure to recognize the lower wetted interface strengths was a larger problem, but, again, it is significant in back calculating properties from the failure and understanding the failure mechanism.
Duncan et al. (2014) summarized subsequent studies which tended to play down the significance of the 3D effects pointing to other uncertainties and noting that it was possible to find 2D cross sections that showed factors of safety of less than one, suggesting that there might have been progressive failure. However, these cross sections had at least some “end effects” and could not fail on their own. And, at least some of the guess work can be eliminated by conducting a 3D analysis in the first place. If this is done using the OMC, a single analysis can also calculate the local factors of safety, as shown in Figure 5(c) indicating locations where progressive failure might start, and repeat analyses can be conducted as desired to follow progressive failure. However, the cases where 3D effects lead to lower factors of safety are not as dramatic and are probably limited in number compared to the cases where 3D effects increase the factor of safety, as shown in the following example.
 Figure 5(c) – Analysis of 3D Problem Showing LFoS from OMC and FoS by Spencer
Figure 5(c) – Analysis of 3D Problem Showing LFoS from OMC and FoS by Spencer
- Puente Hills Canyon 9 Design
A more graphic example of the positive effects of 3D geometry is provided by the Puente Hills Canyon 9 landfill of the Sanitation Districts of Los Angeles County, which happens to have triggered the development of the 3D approach used in the current version of TSLOPE. Canyon 9 represented an expansion of an existing landfill so that one side of the expanded facility consisted of existing compacted municipal solid waste (MSW) that sat on natural ground without a liner. However, new regulations required that both the floor and the slopes of the expansion be placed on a single HDPE liner. Over the floor the HDPE liner was placed on top of a compacted clay layer that had a lower strength than the interface of a roughened HDPE liner and the MSW, so that sliding along the floor was controlled by the undrained strength of the clay layer (c = 250 psf; φ = 13.5 degrees). However, on the slopes, a smooth HDPE liner was placed directly on the slopes excavated in the in situ soft rock and the weakest interface was judged to be the contact between the liner and the MSW (c = 0; φ = 10 degrees) because the liner was anchored into the in situ material on a number of benches. Thus, there were three zones of the base of the landfill that had different strengths for the purpose of analysis, although 2D analyses of sections that passed through the mouth of the canyon, such as shown in Figures 6(a) and (b), suggested that the critical 2D section involved sliding only on the floor and the slopes and did not involve the existing MSW (assumed at the time to have a shear strength of c = 0; φ = 30 degrees). However, when construction was well advanced, a leading geotechnical consultant who was brought in to perform the analyses of slope stability that were required by regulators, found, not surprisingly, that the conventional 2D factor of safety of a section passing through the mouth of the canyon was only 1.22 – less than the required minimum – and, more surprisingly, found that an early, commercially available 3D slope stability program gave similar results.
 Figure 6(a) – 2D Cross Section through Mouth of Canyon
Figure 6(a) – 2D Cross Section through Mouth of Canyon
Figure 6(b) – 3D View of Base of Canyon
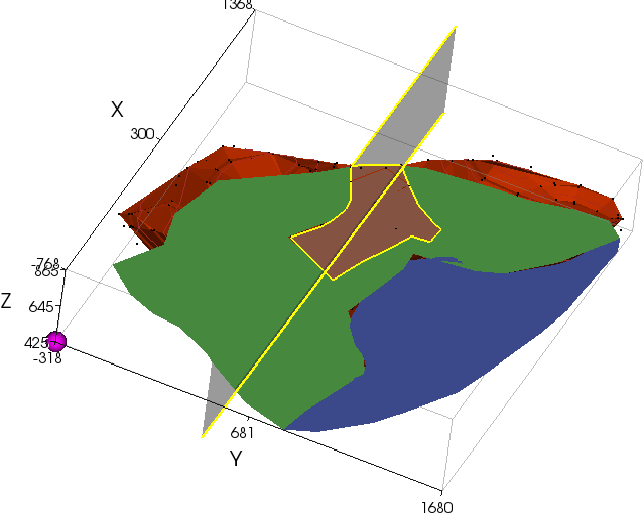
The owner, justifiably, threw a flag at this point because it was evident that in a “bottleneck” canyon like this, as shown in Figure 6(b), the 3D effects had to be significant with the mouth of a canyon acting like the abutments of a good arch dam site. The upshot of this was that another geotechnical consultant brought in the writer to develop and use a program that more properly modelled the 3D geometry and its effects. The original program, variously called TSLOPE3 or T3, used a horizontal force equilibrium solution which Los Angeles County had for some years required geotechnical consultants to perform by hand. The properties cited above were assigned over the basal surface as shown in Figure 6(c), where the red zone is the floor of the canyon, the green zone is slopes lined with HDPE, and the blue zone is the adjacent MSW. Using the original program, a factor of safety of 1.92 was obtained, more than satisfying the regulatory requirement of a factor of safety of 1.5. The updated program, now called just TSLOPE, gives a factor of safety or 1.70 using the OMC and, by chance, gives a factor of safety of 1.93 using Spencer’s Method.
Figure 6(c) – 3D View Showing Zones with Different Properties
As in other problems, the higher factor of safety by Spencer’s Method is consistent with the implication of a rigid body which is restrained even more by the bottle-neck than is the OMC model which assumes that each column can move independently. The fact that the Los Angeles County horizontal force equilibrium method and Spencer’s method give almost identically the same factor of safety for this problem is a fluke, rather than an indication of a fundamental truth. The local factors of safety computed using the OMC are shown in Figure 6(d). In this figure the blue colours indicate a negative factor of safety or, in other words, a reverse slope. Basically, the abutments and the floor of the canyon are holding the MSW up while it tries to slide down the back slope. The 2D factors of safety for the section shown in Figure 6(a) are 1.20 by the OMC and 1.22 by Spencer’s Method, so that the 3D analyses show increases of 42 percent and 58 percent over the 2D analyses.
Figure 6(d) – Local Factors of Safety in 3D Analysis
The fact that there is a significant 3D effect for this problem, or for a dam in a narrow canyon, should come as no surprise, but, again, what turns out to be surprising is that there can also be significant 3D effects in real life problems where it would normally be thought that a 2D analysis of a slope with a constant cross section suffices. This can happen where a 2D potential failure surface dives under a wall or a revetment whereas in reality the failure has to cut through the wall or revetment, as shown in the following example.
- Treasure Island
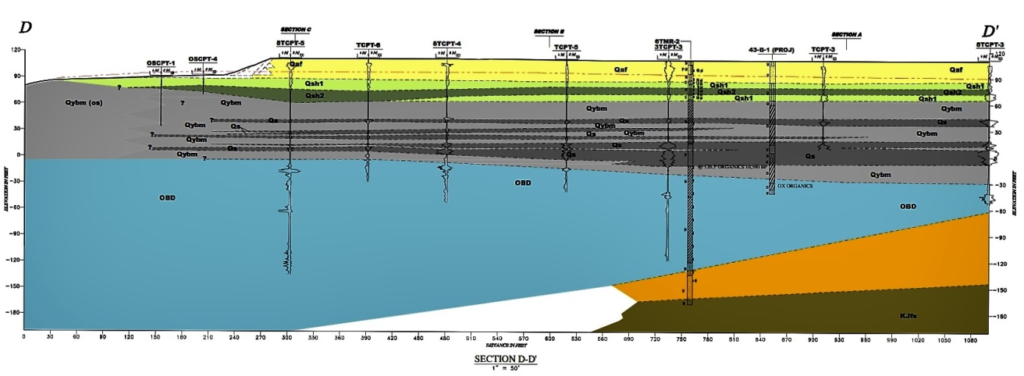
Treasure Island, a man-made island in San Francisco Bay, was originally intended to serve as an airport, but, after the completion of the 1939 World’s Fair, the island was taken over by the US Navy. It is presently being redeveloped for civilian use. The sand fill that was place to form the island will be densified to mitigate possible liquefaction and the final grades will be raised up to 5 feet to allow gravity flow of stormwater for the foreseeable future. Prefabricated vertical drains and surcharging will be used to limit future settlement of the underlying young Bay Mud. The cross section below and the soil properties are taken from publicly-released bid documents.
Figure 7(a) – Section D-D’
The shoal materials which underlie the sand fill are clayey sands that generally contain from 15 to 30 percent fines. These materials are not liquefiable in any conventional sense and they were very resistant to densification by vibratory loading in trials that were performed at the site. Thus, with the young Bay Mud consolidated not only under the weight of the existing fill but under additional surcharge loads and the rock revetment is composed of free-draining, competent rock, there is no obvious concern about shoreline stability at this site, even given its proximity to the San Andreas and Hayward faults.
Nonetheless, in the bid documents there were brief descriptions of work done by the project’s geotechnical consultant using simplified methods of analysis which indicated a potential shoreline stability problem. This raised the question of whether there is any screening analysis that is appropriate for this site. The short answer is yes, there is. As explained by Harry Seed in his Rankine lecture (Seed, 1979), for materials that do not undergo a loss of strength and stiffness as a result of cyclic loading, pseudo-static analyses are not too bad. And pseudo-static analyses are also required to compute the yield acceleration (the seismic coefficient that reduces the factor of safety to unity – the factor of safety for a specified seismic coefficient can then be derived from this) for use in the various simplified methods to compute deformations.
TSLOPE was used to compute the static factors of safety and the yield acceleration for both 2D and 3D slip surfaces. For Section D-D’, when a circular slip circle is transformed to a spherical or ellipsoidal slip surface, two things happen. One is that the slip surface now has to cut through the rock revetment, rather than diving under it – this will increase the factor of safety. The other is that relatively more of the slip surface will be in the young Bay Mud – this might either reduce or increase the factor of safety, depending on the strength of the Bay Mud relative to the other materials that are involved.
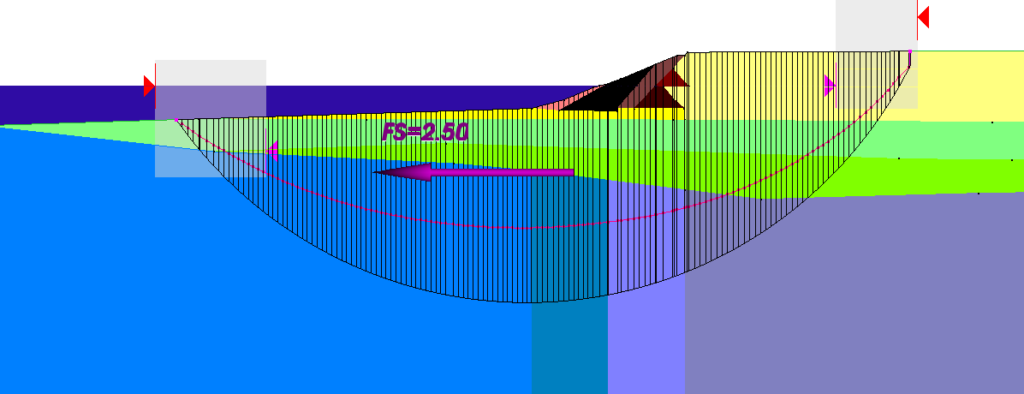
For the “seismic” loading case undrained strengths were used for all materials below the water table, except for the rockfill in the revetment. These strengths were also corrected for rate of loading effects in order to represent the short rise time of an earthquake pulse. The critical circular slip surfaces obtained using Spencer’s Method and the “static” and “seismic” properties are shown in Figures 7(b) and (c).
Figure 7(b) – Section D-D’ Static Analysis
Figure 7(c) – Section D-D’ Static Analysis with “Seismic” Properties
These are both for “static” analyses without the application of a seismic coefficient. The critical circular slip surface obtained in the “static” analysis with “seismic” properties was then used in subsequent searches for the yield acceleration.
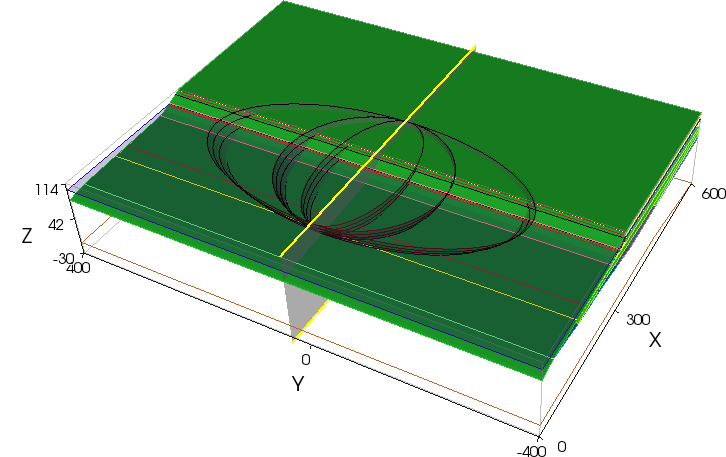
The critical 2D failure surface was also used as the basis for constructing three 3D failure surfaces, as shown in Figure 7(d). The centre 3D slip surface is a sphere, which has an aspect ratio of 1.0. In addition, there are two further ellipsoids that have aspect ratios of 0.5 and 2.0. The larger the aspect ratio, the more the 3D solution approaches the 2 D solution. The results are shown in Table 7.
Figure 7(d) – 3D Potential Failure Surfaces
Table 7 – 2D and 3D Factors of Safety and Yield Accelerations
Again, the reason that the 3D factors of safety are higher than the 2D is that in 3D you must cut through the revetment, rather than diving under it as happens in 2D. Of the four cases, the one with the aspect ratio of 0.5, which gives the highest factor of safety, is probably the most like a typical landslide.
As expected for a slope that has been stable for many years and would have been at greatest risk at the end of construction, the static factors of safety are healthy enough and the yield accelerations are great enough relative to the design peak ground acceleration of 0.46g to suggest any deformations under earthquake loadings would be quite small.
This example strongly suggests that simplified analyses using conventional procedures and 2D slope stability analyses can be unnecessarily conservative in some cases, and as in this particular case, suggest that there is a problem where no problem actually exists.
Conclusions
- 3D geometry can occasionally reduce the calculated factor of safety, but more usually it increases the calculated factor of safety. The increase is up to as much as 60 percent in the examples that are shown.
- You will never know how much difference it makes on your project unless you check.
- However, it is still true that even with the best tools, the engineer still must exercise his or her own judgment!
References
Baligh, M.M., and Azzouz, A.S., “End Effects on Cohesive Slopes”, Journal of Geotechnical Engineering, ASCE, Volume 101, No. 11, 1975
Ching, R.K.H., and Fredlund, D.G., “Some difficulties associated with the limit equilibrium method of slices”, Canadian Geotechnical Journal, Vol. 20, pp. 661-672, 1983
Duncan, J.M., Wright, S.G. and Brandon, T.L. “Soil Strength and Slope Stability, 2nd Edition”, ISBN: 978-1-118-65165-0, Wiley, September 2014
Hovland, H.J., “Three-dimensional slope stability analysis method”, Journal of the Geotechnical Engineering Division of ASCE, Vol. 103, No. 9, 1977
Hungr, O., Salgado, F.M. and Byrne, P.M., “Evaluation of a Three-Dimensional Method of Slope Stability Analysis”, Canadian Geotechnical Journal, Vol. 26, pp. 679-686, 1989
King, G.J.W., “Revision of the effective-stress method of slices”, Geotechnique, Vol. 39, No. 3, 1988
Krahn, J., “The 2001 R.M. Hardy lecture: The limits of limit equilibrium analysis”, Canadian Geotechnical Journal, Vol. 40, pp. 643-660. 2003
Mitchell, J.K., Seed, R.B., and Seed, H.B., “Kettleman Hills Waste Landfill Slope Failure I: Liner System Properties”, Journal of Geotechnical Engineering, Volume 116, No.4, pp. 647-668, 1990
Morgenstern, N.R., and Price, V.E., “The Analysis of the Stability of General Slip Surfaces”, Geotechnique, Vol. 15, No. 1, pp.79-93, 1965
Pyke, R., “Normal Stresses, Seepage Forces and Pond Pressures in the Method of Slices or Columns”, http://rpce.us, April 2017(a)
Pyke, R., “Pros and Cons of the Analysis of Slope Stability by Various Methods of Slices or Columns”, http://rpce.us, April 2017(b)
Seed, H.B., “Nineteenth Rankine Lecture: Considerations in the Earthquake Resistant Design of Earth and Rockfill Dams”, Geotechnique, Vol.24, No.3, September 1979
Seed, R.B., Mitchell, J.K., and Seed, H.B., “Kettleman Hills Waste Landfill Slope Failure II: Stability Analyses”, Journal of Geotechnical Engineering, Volume 116, No. 4, pp. 669–690, 199
Spencer, E., “A Method of Analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces”, Geotechnique, Vol. 17, No. 1, pp. 11-26, 1967
Whitman, R.V. and Bailey W.A., “Use of Computers for Slope Stability Analysis.” Proc. ASCE, Vol. 93, No. SM4, July 1967
Wright, S.G., H. Bolton Seed Lecture, 2013 (https://www.youtube.com/watch?v=Q_6aOU7msBM)