By Robert Pyke Ph.D., G.E.
The history of slope stability analyses by the method of slices or columns in geotechnical engineering is well documented in the textbook by Duncan, Wright and Brandon (2014) and elsewhere. The procedures used for slope stability analysis started out as hand or graphical methods, but with the introduction of limit equilibrium methods of analysis most calculations became computerized. Many engineers seem to believe that these computer programs automatically give the correct answer, but, in addition to the “garbage in – garbage out” rule still holding, these analyses are simplified and thus approximate at best. There are also specific features of the common methods of analysis that may limit their usefulness in various ways.
To start with, there are two ways that the factor of safety has been defined in the analysis of slope stability using the method of slices or columns.
The first is the simple definition that the factor of safety is the sum of the resisting forces around the failure plane divided by the sum of the driving forces. This was used in early analyses using the method of slices and many geotechnical engineers appear to still believe that this is the way the factor of safety is calculated.
However, most modern computer programs define the factor of safety differently, as a strength reduction factor. The factor of safety is that factor by which the assumed shear strengths must be reduced in order that the sums of the driving and resisting forces are equal.
A common argument in support of this definition is that the shear strengths around the failure plane are the greatest source of uncertainty in the analysis, so that it makes sense to factor the shear strengths. That is questionable. In practice, most geotechnical engineers adopt conservative values for the shear strengths or shear strength parameters, so that the uncertainty in these values is already considered. A better, contrary, argument is that the methods that define the factor of safety this way force the factor of safety to be the same at the base of each slice and obscure the fact that some parts of the potential slip surface may be overstressed, even if the overall factor of safety is above 1.0. That is a good reason for normally requiring an overall factor of safety of 1.5 in practice. If the factor of safety is 1.5 or greater, then the local factors of safety are less likely to fall below 1.0 and the risk of progressive failure should be diminished. Also, as shown in a separate article, the omission of seepage forces in limit equilibrium methods of analysis can cause the factor of safety to be overestimated by as much as 30 percent, so that is yet another reason for requiring a factor of safety of 1.5. On the other hand, 3D effects, while they can in some cases reduce the factor of safety, normally increase it, sometimes very significantly, so that requiring a 2D factor of safety of 1.5 for those cases may be excessive.
Using the second definition of the factor of safety, the sums of the driving and resisting forces are made equal, therefore the methods of analysis that use it are called “limit equilibrium analyses”. Some methods of analysis, such as Bishop’s Simplified Method, are limit equilibrium analyses but they do not “fully satisfy equilibrium”, meaning that force and moment equilibrium is not fully satisfied for each slice or column and thus for the potential sliding mass as a whole. Methods which do “fully satisfy equilibrium” such as those of Morgenstern and Price (1965) or Spencer (1967) are now generally preferred by both academics and practitioners.
The principal direct implication of how the factor of safety is defined is that with the first, simple definition one can calculate “local factors of safety” for each slice or column whereas in limit equilibrium analyses, one cannot do that. Equations of equilibrium are set up and then solved for two unknowns – the factor of safety and a second unknown which usually has to do with the assumptions made regarding side forces acting on the slices of columns. In Spencer’s Method this unknown is the angle of inclination of the side forces, which is assumed to be constant for all slices or columns. In the Morgenstern and Price method it is a scale factor for the side forces whose varying angles of inclination are specified by the user.
Again, with the second definition of the factor of safety there is only one factor of safety and it applies to each slice or column as well as the overall potential sliding mass. As noted already, this obscures the fact that some segments of the potential slip surface are likely closer to failure than others, but it also forces an at least somewhat artificial distribution of the normal and shear stresses around the potential slip surface. The normal stresses will impact the shear strengths calculated for non-cohesive materials, that is, materials for which the strength is at least in part specified to be a function of the normal stress on the potential slip surface. This is demonstrated subsequently in several examples which show the normal stress distributions obtained using limit equilibrium analyses and a simple method of analysis which is not a limit equilibrium analysis. It turns out that the difference in the normal stresses is the big contributing factor to any differences in the factor of safety that are computed by the two methods.
Given the previous discussion, one might then ask, “why do people generally prefer methods that fully satisfy equilibrium?” The basic answer to this question seems to be that engineers are taught in undergraduate classes that any analysis of the stresses in a rigid body should “fully satisfy equilibrium”, and it certainly looks more elegant or sophisticated to do this. But is it correct for a potential sliding mass that is deformable and can’t take tension?
The second definition of the factor of safety and the quest to fully satisfy equilibrium implies that the potential sliding mass acts as a rigid body. Leaving aside for the moment whether this is reasonable or not for real slopes, this forces the factor of safety to be the same for all slices, and, as already noted, forces an at least somewhat artificial distribution of the normal and shear stresses around the potential slip surface, but it has other implications as well. These implications have to do with the development of tensile interslice forces and the calculated line of thrust, and also whether or not the solution converges and, further, whether or not it converges to the correct solution.
Solutions that “fully satisfy equilibrium” will tend to develop negative interslice forces wherever there is a hump in the potential slip surface and at the upper end of a shallow potential slip surface. The computed factors of safety in these cases may be quite unconservative because the assumed rigid body gets hung up. Thus, the user needs to insert tension cracks as necessary to eliminate any tensile interslice forces, since soil and rock masses generally have no tensile capacity. The user also then has to decide whether a model with perhaps artificially deep tension cracks is real or not.
More attention in the literature has been applied to the line of thrust, that is the locus of the points of application of the interslice forces, and this has generally been the principal recommended test for whether a solution is reasonable or not. Ideally the line of thrust should be located at something like the third point of the slices or columns but it should never travel outside the boundaries of the potential sliding mass, as it commonly does in problems with tensile interslice forces and sometimes does in pseudo-static seismic analyses.
The occurrence of tensile interslice forces and odd lines of thrust is illustrated using the example of a relatively simple embankment dam, but it is also helpful to compare the results using a method that “fully satisfies equilibrium”, in this case Spencer’s Method, with a method that uses the first, simple definition of the factor of safety, in this case the Ordinary Method of Columns (OMC), a 3D implementation of the Ordinary Method of Slices (OMS). The OMC and some past criticisms of the OMS will be described in more detail in a subsequent article, but for this example, it is sufficient to say that it uses the first definition of the factor of safety and that interslice, or intercolumn, forces are neglected. It is as if a bunch of square columns coated with Teflon can slide up and down as the overall slope deforms. Thus, the OMC implies that the potential sliding mass is deformable whereas Spencer’s method implies that the potential sliding mass is rigid.
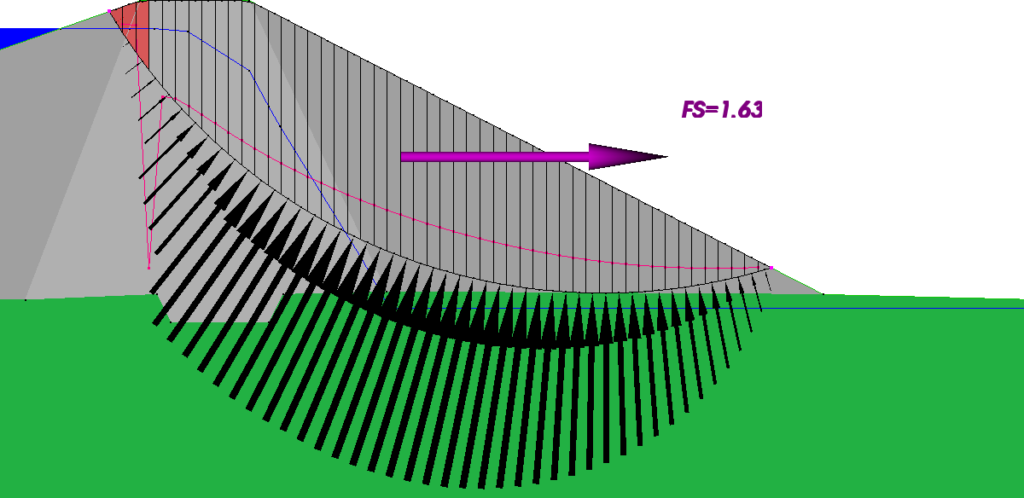
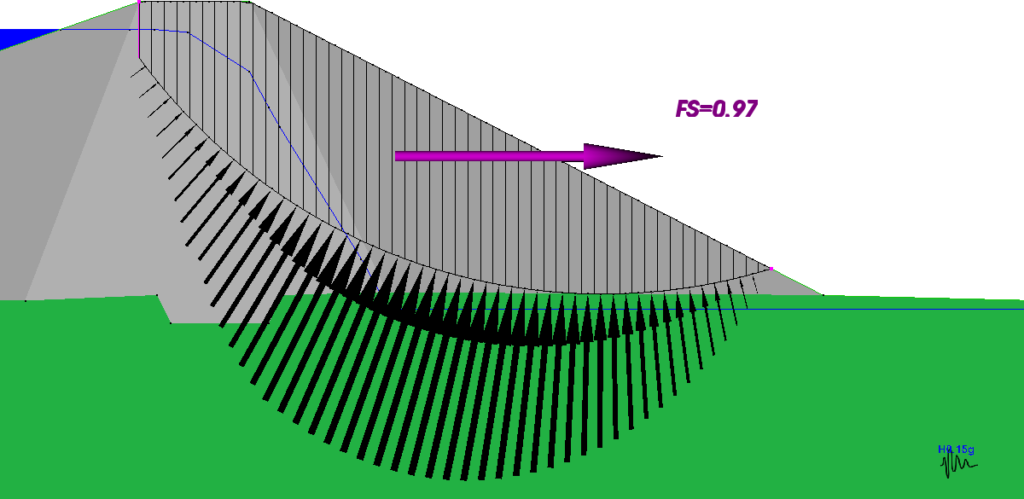
Figure 1 shows results for the stability of the downstream slope of a simple dam embankment analysed using both Spencer’s Method and the OMC. In Figure 1(a) using Spencer’s Method causes the development of tensile interslice forces, indicated by slices coloured red, and causes the line of thrust, shown as a red line, to swing outside the potential sliding mass.
Figure 1(a) – No Tension Crack, Spencer
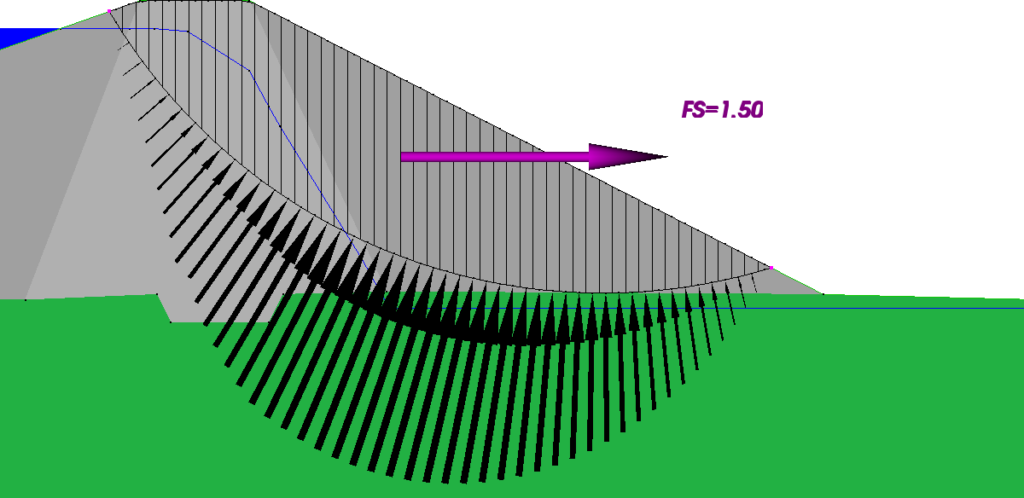
Figure 1(b) – No Tension Crack, OMC
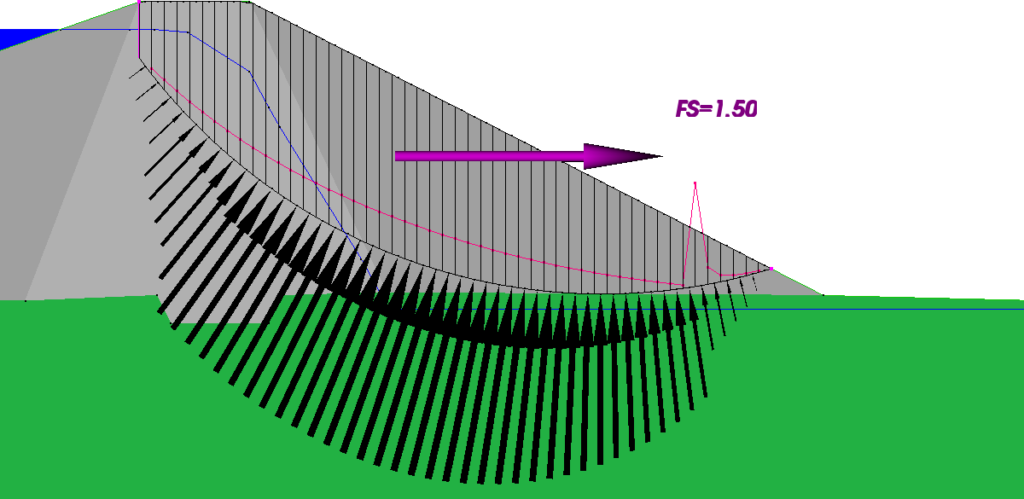
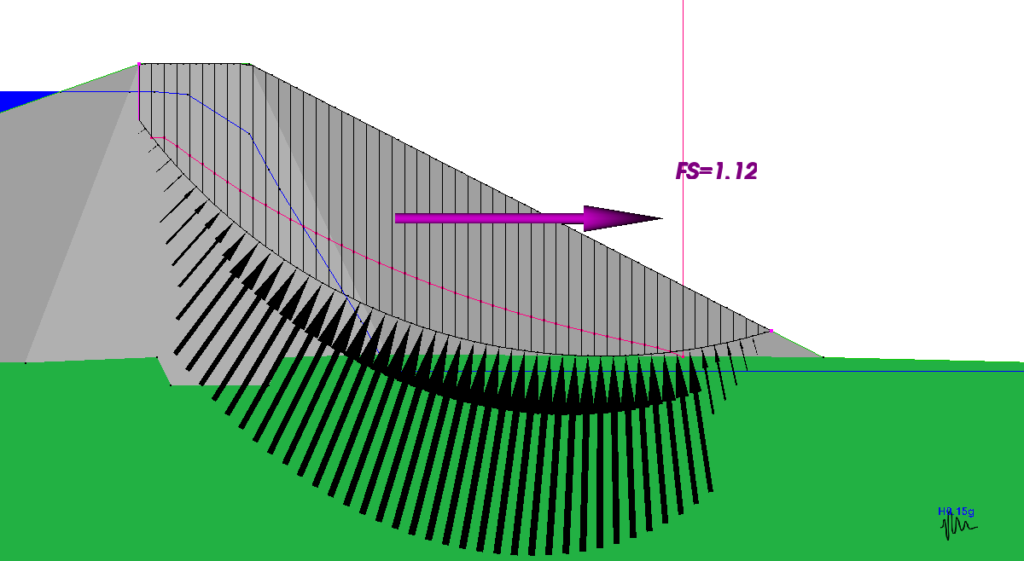
In Figure 1(c), the tensile interslice forces in the solution by Spencer’s method have been eliminated by inserting a tension crack, slightly lowering the computed factor of safety. However, instead of the line of thrust going way outside of the potential sliding mass at the top of the slope, it now has a hiccup at the toe.
Figure 1(c) – With Tension Crack, Spencer
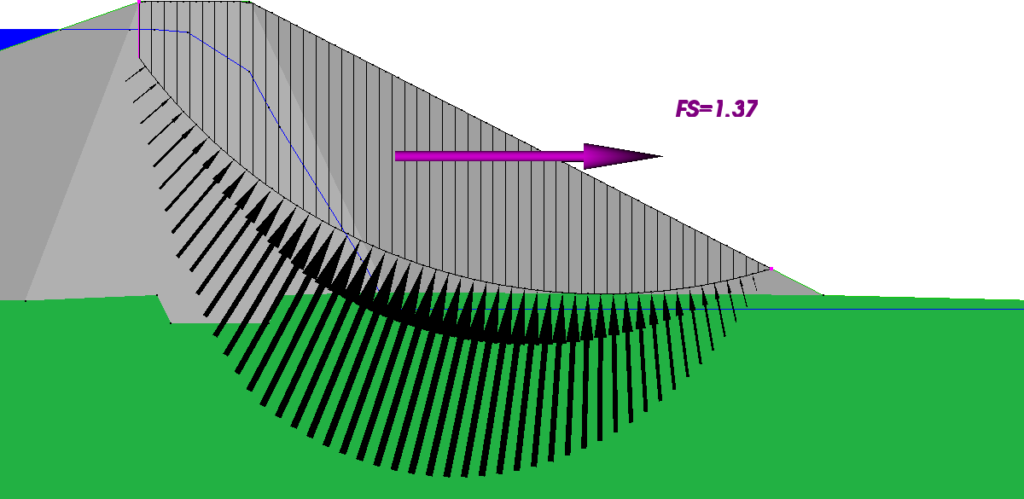
Figure 1(d) – With Tension Crack, OMC
Note that in both Figures 1(b) and 1(d), the OMC gives a lower factor of safety than Spencer’s method. This is partly because Spencer’s method does not account for seepage forces, but the seepage forces in this problem are not very large relative to the gravity forces and most of the difference results from the difference in the distribution of the normal stresses on the bases of the columns. In this problem both the core and the downstream shell are specified to have shear strengths with both cohesive and non-cohesive components and the non-cohesive component is sensitive to the normal forces. The normal forces in the figures have different scales because the scale is set so that the maximum values have the same length, but the vector sums of the normal forces are equal. However, with Spencer’s method more of the load is transferred towards the ends of the slip surface and, overall, this increases the shear strengths and the factor of safety. With the OMC there is no internal load transfer and the normal stress results solely from the weight of the column in question. The truth likely lies somewhere in between these two extremes. If the shear strengths are specified entirely as cohesions and there are no seepage forces, that is, the water conditions are hydrostatic, the companion article on the inclusion of seepage forces shows that the OMC and Spencer’s method give identical results.
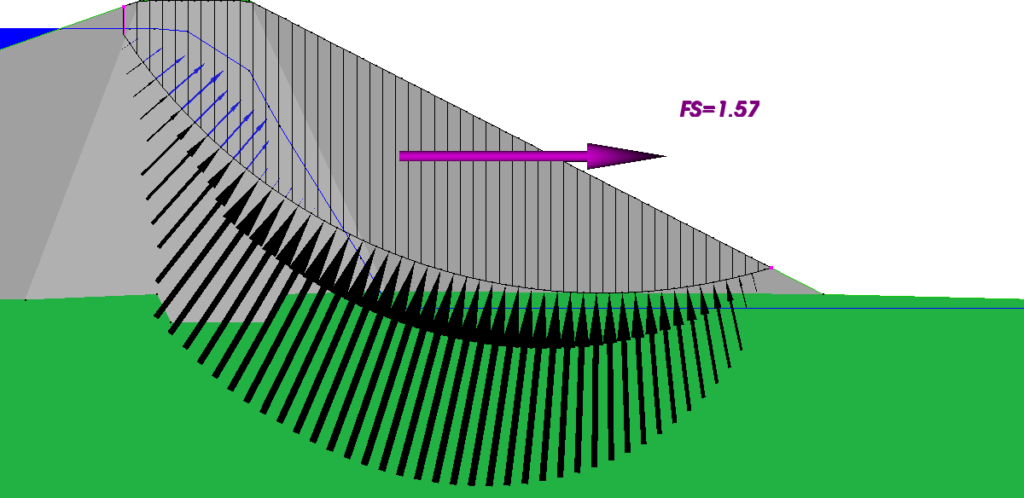
If the engineer is troubled by the line of thrust in Figure 1(c) and wants to spend more time on the problem, it can be eliminated by halving the depth of the tension crack, as shown in Figure 1(e). The resulting factor of safety of 1.57 might be considered the “best answer” by many authorities, but the corresponding value of 1.44 by the OMC is a safer and likely more realistic value, given that the dam embankment is not rigid and must be subject to some seepage forces.
Figure 1(e) – With Shorter Tension Crack, Spencer
The difficulty of obtaining what Morgenstern and Price called a “physically acceptable” solution, without tension and with the line of thrust contained within the potential sliding mass, using Spencer’s method illustrates the importance of the user being able to readily see the line of thrust and the occurrence of tension.
Figures 1(f) and 1(g) illustrate how these problems can be compounded by the addition of external loads such as pseudo-static seismic forces. In Figure 1(f) the problem with the line of thrust seen in Figure 1(c) is now aggravated. It is not uncommon for the line of thrust in pseudo-static analyses using methods that fully satisfy equilibrium to come out of the slope and the engineer must decide whether he/she can live with that or not. In the corresponding analysis by the OMC, the normal stresses on the bases of the columns are not impacted by the added seismic loads so that a nicer looking distribution of the normal forces are obtained and the same shear strengths apply around the slip surface as were used in the static analysis. But, pseudo-static analyses are approximate anyway and these points are less important than whether standard static strength properties are used or whether adjustments, which might be considerable, are made for different drainage conditions and rates of loading.
Figure 1(f) – With Tension Crack and Seismic Coefficient, Spencer
Figure 1(g) – With Tension Crack and Seismic Coefficient, OMC
This question of the reasonableness of the results of slope stability analyses obtained using the various forms of the method of slices has been repeatedly addressed in the literature but, sadly, it is often ignored in practice. Morgenstern and Price (1965), in their very elegant paper which introduced the concept of a user-specified distribution of the angle of inclination, emphasized that there were multiple possible solutions and that the user should vary the assumed distribution of the angle of inclination so that a reasonable line of thrust was achieved, if possible. Whitman and Bailey (1967), who correctly took Morgenstern and Price to be the gold standard for analyses that fully satisfy equilibrium, said “the use of the Morgenstern-Price approach together with a computer does not free the engineer from making a judgment concerning the reasonableness of a solution.” Chin and Fredland (1983) noted some difficulties with methods that fully satisfy equilibrium, including the fact that they sometimes have trouble converging to a solution, and suggest some possible workarounds. Krahn (2003) discussed the limits of limit equilibrium analyses including convergence issues and difficulties with applying external forces. He suggested that the latter can best be addressed using a hybrid finite element – limit equilibrium analysis but that seems unwieldy for routine use.
Wright (2013), in a “must watch” lecture, included several case histories that illustrate various problems with methods that fully satisfy equilibrium. Wright emphasized that there is no absolutely correct solution, and suggested that the engineer should always use at least two computer programs for any critical problem, in part because computer programs may include hidden assumptions and also may not show the intermediate results that are necessary to judge the reasonableness of the final result. Or, as an alternative, the engineer can use one program that offers two good methods of solution and makes all the key data visible.
References
Baligh, M.M., and Azzouz, A.S., “End Effects on Cohesive Slopes”, Journal of Geotechnical Engineering, ASCE, Volume 101, No. 11, 1975
Ching, R.K.H., and Fredlund, D.G., “Some difficulties associated with the limit equilibrium method of slices”, Canadian Geotechnical Journal, Vol. 20, pp. 661-672, 1983
Duncan, J.M., Wright, S.G. and Brandon, T.L. “Soil Strength and Slope Stability, 2nd Edition”, ISBN: 978-1-118-65165-0, Wiley, September 2014
Hovland, H.J., “Three-dimensional slope stability analysis method”, Journal of the Geotechnical Engineering Division of ASCE, Vol. 103, No. 9, 1977
Hungr, O., Salgado, F.M. and Byrne, P.M., “Evaluation of a Three-Dimensional Method of Slope Stability Analysis”, Canadian Geotechnical Journal, Vol. 26, pp. 679-686, 1989
King, G.J.W., “Revision of the effective-stress method of slices”, Geotechnique, Vol. 39, No. 3, 1988
Krahn, J., “The 2001 R.M. Hardy lecture: The limits of limit equilibrium analysis”, Canadian Geotechnical Journal, Vol. 40, pp. 643-660. 2003
Mitchell, J.K., Seed, R.B., and Seed, H.B., “Kettleman Hills Waste Landfill Slope Failure I: Liner System Properties”, Journal of Geotechnical Engineering, Volume 116, No.4, pp. 647-668, 1990
Morgenstern, N.R., and Price, V.E., “The Analysis of the Stability of General Slip Surfaces”, Geotechnique, Vol. 15, No. 1, pp.79-93, 1965
Pyke, R., “Normal Stresses, Seepage Forces and Pond Pressures in the Method of Slices or Columns”, http://rpce.us, April 2017
Seed, H.B., “Nineteenth Rankine Lecture: Considerations in the Earthquake Resistant Design of Earth and Rockfill Dams”, Geotechnique, Vol.24, No.3, September 1979
Seed, R.B., Mitchell, J.K., and Seed, H.B., “Kettleman Hills Waste Landfill Slope Failure II: Stability Analyses”, Journal of Geotechnical Engineering, Volume 116, No. 4, pp. 669–690, 1990
Spencer, E., “A Method of Analysis of the Stability of Embankments Assuming Parallel Inter-Slice Forces”, Geotechnique, Vol. 17, No. 1, pp. 11-26, 1967
Whitman, R.V. and Bailey, W.A., “Use of Computers for Slope Stability Analysis”, Journal of Geotechnical Engineering, Vol. 93, No. SM$, July 1967
Wright, S.G., H. Bolton Seed Lecture, 2013