By Robert Pyke Ph.D., G.E.
Analyses of seismic slope stability problems using limit equilibrium methods in which the inertia forces due to earthquake shaking are represented by a constant horizontal force (equal to the weight of the potential sliding mass multiplied by a coefficient) are commonly referred to as pseudo-static analyses.
They are relatively simple to perform but involve many approximations. They should not be used at all when the materials involved might undergo a significant loss of strength under earthquake shaking and should always be used with caution.
The most common mistake made in using such analyses does not in fact yield unconservative results, but rather the opposite. This mistake consists of using the expected peak horizontal acceleration as the seismic coefficient.
In the absence of a dramatic loss of strength, this must yield excessively conservative results since the peak acceleration acts only momentarily in one direction.
However, if it is overly conservative to use the expected peak acceleration, what value should be used and can it be related to the peak acceleration?
In recent years a basic point of reference has been the U.S. Army Corps of Engineers manual for seismic design of new dams (which are generally considered to be among the more critical civil engineering facilities). This requires use of a seismic coefficient of 0.1 in Seismic Zone 3 and 0.15 in Seismic Zone 4, in conjunction with a minimum factor of safety of 1.0.
In California, many state and local agencies also require the use of a seismic coefficient of 0.15 but impose the slightly more conservative requirement that the minimum computed factor of safety be not less than 1.1.
Clearly, however, engineering judgement must still be applied as to the applicability of pseudo-static analyses and the acceptable factor of safety might be varied with the uncertainties involved in a particular analysis.
Further, it is now possible to make an approximate but rational connection between the seismic coefficient that is used in a pseudo-static stability analysis and the expected amplitudes and duration of ground motion by working backwards through the method for computing displacements of slopes that was originally suggested by Newmark (1965).
This approach was first explored by Seed (1979) who drew the general conclusion that for embankments composed of materials which show no significant loss of strength as a result of cyclic loading, "it is only necessary to perform a pseudo-static analysis for a seismic coefficient of 0.1 for magnitude 6.5 earthquakes or 0.15 for magnitude 8.25 earthquakes and obtain a factor of safety of the order of 1.15 to ensure that displacements will be acceptably small".
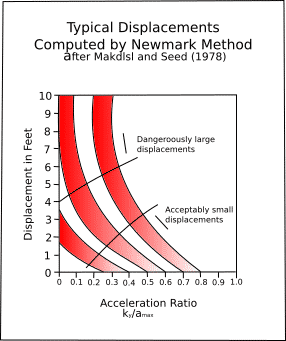
While Seed simplified his conclusion to make it independent of the peak acceleration, the procedure that he suggested can be used to make more site specific evaluations of appropriate seismic coefficients by referring to Figure 1, which is based on the same study by Makdisi and Seed (1978) that Seed used in his 1979 lecture and paper.
The figure shows displacements computed by the Newmark method (specifically for embankments ranging in height from 50 to 250 feet, but generally applicable to earth slopes with depths to bedrock in that order, and generally conservative for shallower depth to bedrock) as a function of the acceleration ratio, ky/amax, where ky is the critical seismic coefficient (that is, the seismic coefficient that reduces the factor of safety to unity) and amax is the expected peak acceleration.
Ranges of the most likely displacements are indicated for magnitudes 6.5, 7.5, and 8.25 (magnitude being an indicator of duration of strong shaking) and likely displacements for intermediate magnitudes can be interpolated.
The predicted displacements should necessarily be small for magnitudes less than about 6.5 since field experience indicates that smaller magnitude, shorter duration earthquakes do not usually cause significant slope failures.
While there are a number of approximations made in the Newmark method and in the construction of Figure 1, if the acceleration ratio and magnitude are such that they fall below the line marked 'acceptably small displacements', the slope involved might generally be considered to be safe from failure.
Thus, for a magnitude 8.25 earthquake, non-failure conditions are indicated if the critical seismic coefficient is at least equal to half the expected peak acceleration.
Conversely, if a pseudo-static analysis using a seismic coefficient equal to one-half the peak acceleration yields a factor of safety greater than 1.0, the displacements are likely to be acceptably small.
Similarly, for magnitude 7.5, 7.0, and 6.5, if the seismic coefficient is taken as one-third, one-fourth and one-fifth of the expected peak acceleration, and the computed factor of safety is greater than 1.0, the displacements are likely to be acceptably small.
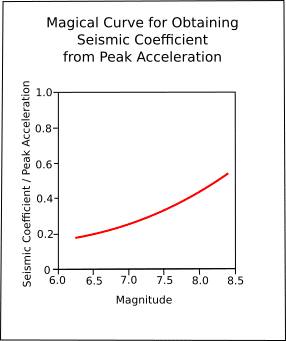
The seismic coefficients obtained this way are shown as a function of peak acceleration and magnitude in Figure 2.